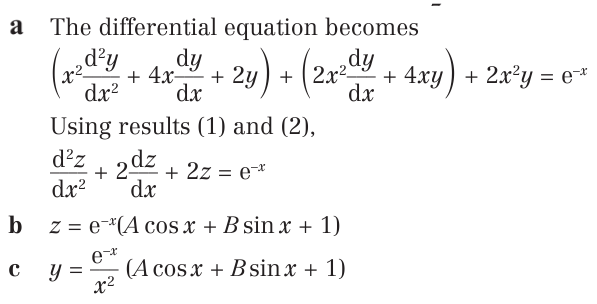Reduce a 2nd-order ODE using substitution 2

Resources on this page:
Generated* SBD with worked solution
*Refresh this page to get a new variation.

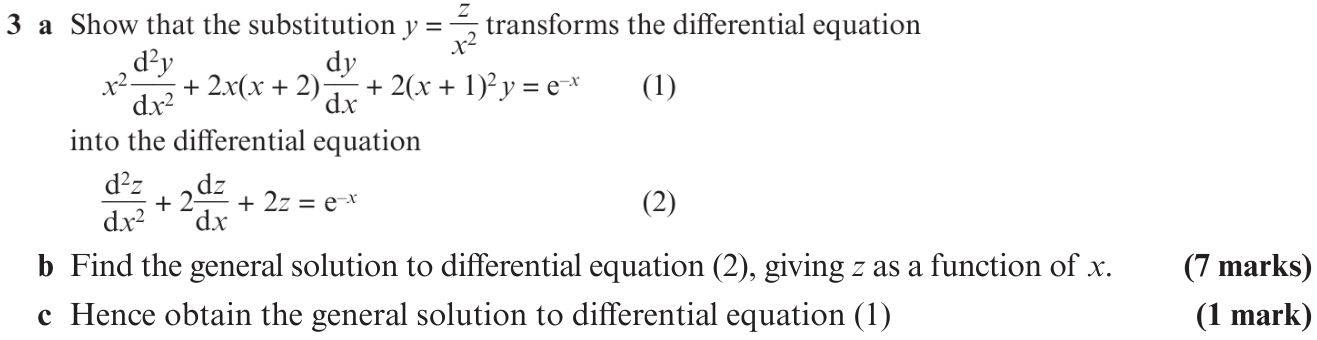
Further Pure 1 Ex 9B Q3 - the answer is at the bottom of this page

Remember: productive practice is perfect preparation

Once you have seen and understood how to do the question then do it yourself
If you used help then after a few days retry the question without help

FP1 Ex 9B Q3 - Generated SBD

$ \newcommand\cosec{{ \,\text{cosec}\, }} \newcommand\fderiv{{ \frac{\text{d}}{\text{d}x} }} \newcommand\fderivy{{ \frac{\text{d}y}{\text{d}x} }} \newcommand\fderivz{{ \frac{\text{d}z}{\text{d}x} }} \newcommand\sderiv{{ \frac{\text{d}^2}{\text{d}x^2} }} \newcommand\sderivy{{ \frac{\text{d}^2y}{\text{d}x^2} }} \newcommand\sderivz{{ \frac{\text{d}^2z}{\text{d}x^2} }} $

(a) Show that the transformation $ y = $ ${z \over x^2} $ transforms the differential equation

\[ x^2 \sderivy + @03 x(@04 @05 x) \fderivy + @06(@07 x^2 @08 x + @09)y = \text{e}^{@02 x} \qquad ...(1) \]

into the differential equation

\[ \sderivz @00 \fderivz + @01 z = \text{e}^{@02 x} \qquad ...(2) \]

(6 marks)

(b) Find the general solution to the differential equation (2), giving $z$ as a function of $x$.

(7 marks)

(1 mark)

Solution

\[\begin{align} &\text{(a) First we need to find the first and second derivatives of the given transformation:} \\\\ & z = x^2 y \qquad ...(3) \\\\ & \fderivz = 2xy + x^2 \fderivy \qquad \implies \qquad x^2 \fderivy = \fderivz - 2xy \qquad ...(4) \\\\ & \sderivz = 2y + 4x \fderivy + x^2 \sderivy \qquad \implies \qquad x^2 \sderivy = \sderivz - 4x \fderivy - 2y \qquad ...(5) \\\\ &\text{Substitute (5) in (1)}. \\\\ & \left( \sderivz - 4x \fderivy - 2y \right) + @03 x(@04 @05 x) \fderivy + @06(@07 x^2 @08 x + @09)y = \text{e}^{@02 x} \\\\ &\text{Collect terms:} \\\\ & \sderivz @00 x^2 \fderivy + @06(@07 x^2 @08 x)y = \text{e}^{@02 x} \\\\ &\text{Substitute for $x^2 \fderivy$ using (4):} \\\\ & \sderivz @00 \left( \fderivz - 2xy \right) + @06(@07 x^2 @08 x)y = \text{e}^{@02 x} \\\\ &\text{Collecting terms again:} \\\\ & \sderivz @00 \fderivz + @01 x^2 y = \text{e}^{@02 x} \\\\ &\text{Substitute for $x^2y$ using (3):} \\\\ & \sderivz @00 \fderivz + @01 z = \text{e}^{@02 x} \qquad \text{as required.} \\\\ \\\\ &\text{(b) Write down the complementary function:} \\\\ & t^2 @00 t + @01 = 0 \\\\ &\text{Use the quadratic formula:}. \\\\ & t = \frac{@10 \pm \sqrt{@11^2 - 4 \times 1 \times @01}}{2 \times 1} \\\\ &\text{This gives us complex roots:} \\\\ & t = @12 \pm @13 i \\\\ &\text{So the particular solution is:} \\\\ & z = \text{e}^{@14x} (A \cos @13 x + B \sin @13 x) \\\\ &\text{We want the general solution, so try $\lambda\text{e}^{@02 x}$ for $z$ in (2):} \\\\ & \sderiv (\lambda\text{e}^{@02 x}) @00 \fderivz (\lambda\text{e}^{@02 x}) + @01 (\lambda\text{e}^{@02 x}) = \text{e}^{@02 x} \\\\ & @15\lambda\text{e}^{@02 x} @16\lambda\text{e}^{@02 x} + @01\lambda\text{e}^{@02 x} = \text{e}^{@02 x} \\\\ &\text{So we have} \quad \lambda = @17 \\\\ &\text{This gives us the general solution:} \\\\ & z = \text{e}^{@14x} (A \cos @13 x + B \sin @13 x @18) @19 \\\\ \\\\ &\text{(c) Substitute for $z$ using (3):} \\\\ & y = {\text{e}^{@14x} \over x^2} (A \cos @13 x + B \sin @13 x @18) @20 \end{align}\]

Answer to the textbook question at the top of this page